3.4 영역

아래 내용은 인사이트 출판사의 제안으로 작성 중인 책의 초고입니다. 실제 출판 시에는 내용이 달라질 수 있습니다. 많은 의견 부탁드립니다.

변수를 식의 어딘가에서 정의했다고 해서 그 변수를 식의 모든 곳에서 사용할 수 있는 것은 아니다. 변수를 사용할 수 있는 곳을 그 변수의 영역(scope)이라고 부른다. 산술x에서 변수를 정의하는 식은 \(x = e_1; e_2\) 꼴이다. 여기서 \(e_2\)는 \(x\)의 영역이지만, \(e_1\)은 \(x\)의 영역이 아니다. 이 점은 변수 정의의 의미를 정의하는 규칙 5를 보면 명확하다.

규칙 5:

\(\ \ \ \ \)\(\sigma\)에서 \(e_1\)의 실행 결과가 \(n_1\)이고

\(\ \ \ \ \)\(\sigma\)에 \(x\)의 값이 \(n_1\)이라는 정보를 추가해 만들어진 환경이 \(\sigma’\)이고

\(\ \ \ \ \)\(\sigma’\)에서 \(e_2\)의 실행 결과가 \(n_2\)이면,

\(\ \ \ \ \)\(\sigma\)에서 \(x = e_1; e_2\)의 실행 결과가 \(n_2\)이다.

\(e_1\)의 실행 결과는 \(\sigma\)에서 계산되므로 \(e_1\)을 계산할 때는 환경에 \(x\)의 값이 없다. 반면, \(e_2\)의 실행 결과는 \(\sigma’\)에서 계산되므로 \(e_2\)를 계산할 때는 환경에 \(x\)의 값이 있다. 그러므로 \(x\)의 영역에는 \(e_2\)만이 포함되는 것이다. 예를 들어 \({\tt x} = {\tt x}; {\tt x}\)라는 식을 생각해 보자. 마지막 \(\tt x\)는 \(\tt x\)의 영역이 맞지만, 두 번째 \(\tt x\)는 \(\tt x\)의 영역이 아니고, 따라서 자유 변수이다. 그러므로 이 식은 계산할 수 없는 식이다.

\(x = e_1; e_2\)에서 \(e_1\)도 \(x\)의 영역에 포함하도록 언어를 고칠 수 있을까? 얼핏 생각하기에 \(e_1\)이 \(x\)의 영역에 포함되는 것은 매우 이상한 일이다. \(x\)의 값을 정하는 식이 \(e_1\)인데 \(e_1\)이 \(x\)를 사용한다니 앞뒤가 맞지 않는다. 그러나 이는 사실 프로그래밍을 해 본 사람이라면 누구나 익숙할 만한 개념으로, \(x\)를 재귀적(recursive)으로 정의하는 것이다. \(x\)의 정의가 자기 자신을 필요로 하므로 \(x\)는 재귀적이다. 하지만 재귀(recursion)는 이번 장에서 다루고자 하는 개념이 아니다. 지금은 산술x의 의미를 그대로 두고 넘어가겠다. 재귀에 대해서는 6장에서 자세히 살펴볼 것이다.

산술x에서 변수의 영역은 그 변수를 정의하는 식을 벗어날 수 없다. 예를 들어, 다음과 같은 산술x 식을 생각해 보자.

\({\tt x} = (\)

\(\ \ {\tt y} = 1;\)

\(\ \ {\tt y}\)

\();\)

\({\tt y}\)

C나 파이썬 같은 명령형 언어(imperative language)에서는 보기 어려운 형태의 식이기 때문에, 위 식이 다소 어색하게 느껴지는 사람도 있을 것이다. 조금 어색할지라도, 산술x에서는 위의 식은 요약 문법을 따르는 식이다. 먼저, \({\tt y} = 1; {\tt y}\)는 앞에서도 많이 본, 변수를 정의하는 \(x = e_1; e_2\) 형태의 식이다. \({\tt y} = 1; {\tt y}\) 역시 \(1 + 2\)나 \(\tt x\) 등과 마찬가지로 하나의 산술x 식이라는 사실을 유의하자. 따라서 다시 \(x = e_1; e_2\) 형태의 식을 만들되, 정의하는 변수의 이름은 \(\tt x\), 그 변수의 값을 정하는 식은 \({\tt y} = 1; {\tt y}\), 변수 \(\tt x\)를 사용하는 식은 \(\tt y\)로 하여 식을 만들면 위의 식이 나온다. 위의 식은 분명히 식의 중간에서 변수 \(\tt y\)를 정의한다. 그러나 마지막 \(\tt y\)는 자유 변수이다. 이는 \(\tt y\)의 영역에는 두 번째 \(\tt y\)만 포함되기 때문이다.

그림과 함께 왜 마지막 \(\tt y\)가 자유 변수인지 알아보자.

시작할 때의 환경은 비어 있다.

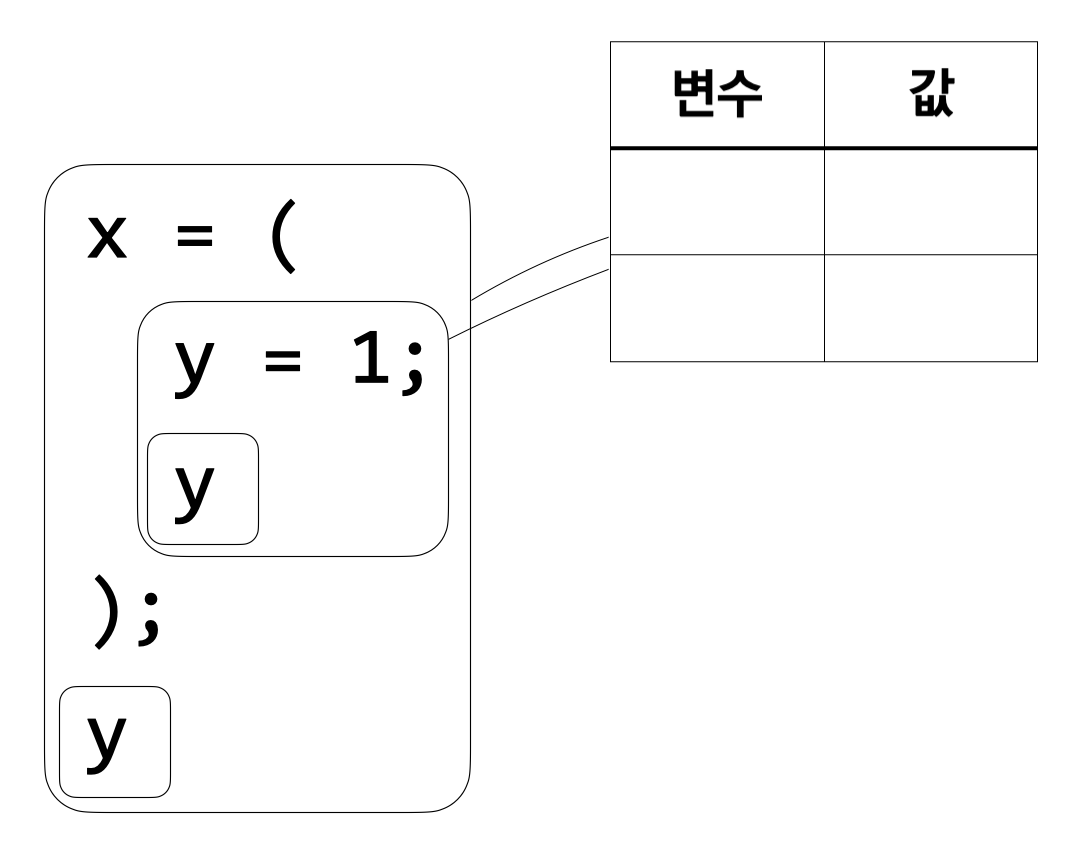
먼저 해야 할 일은 \({\tt y} = 1; {\tt y}\)를 계산하는 것이다. 아직 아무 변수도 정의하지 않았으니 이 식을 계산하는 것 역시 빈 환경에서 이루어진다.

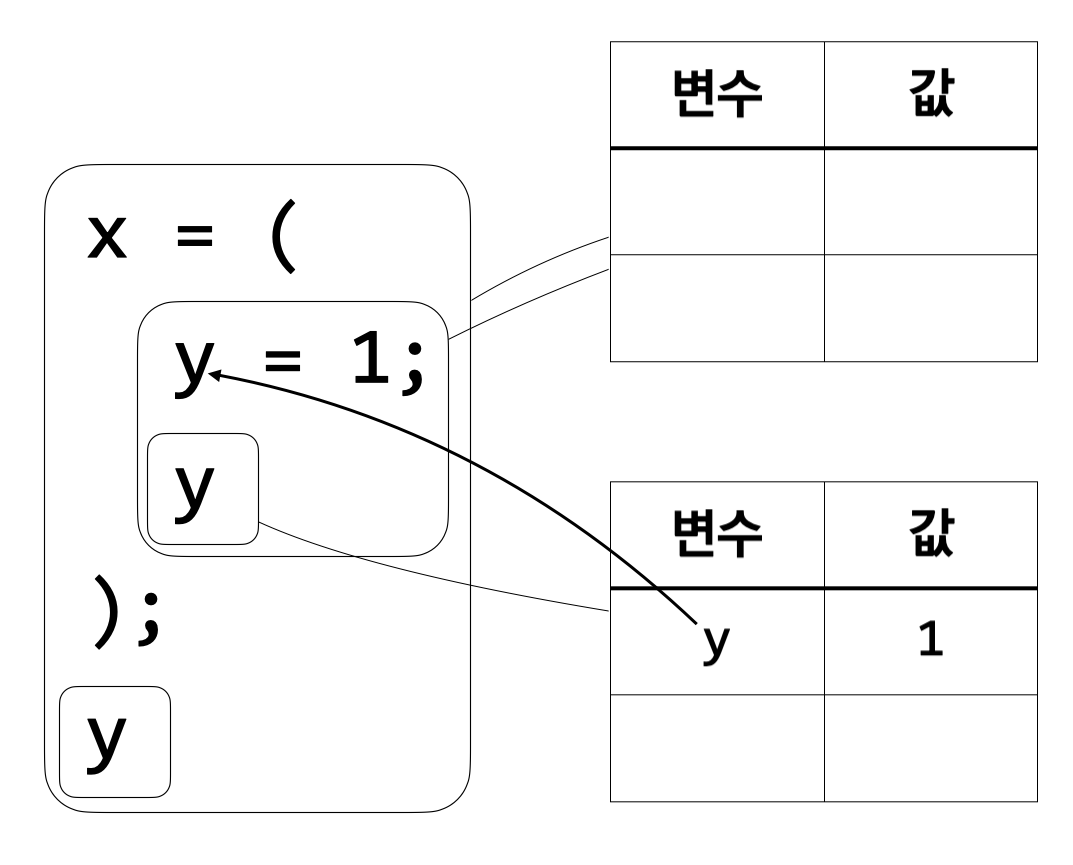
\({\tt y} = 1\)에 따라 변수 \(\tt y\)의 값은 1이다. \(\tt y\)의 값은 두 번째 \(\tt y\)를 계산할 때 사용할 수 있다. 이를 위해 새로운 환경을 만들고 그 환경에 \(\tt y\)의 값이 1이라는 정보를 저장한다.

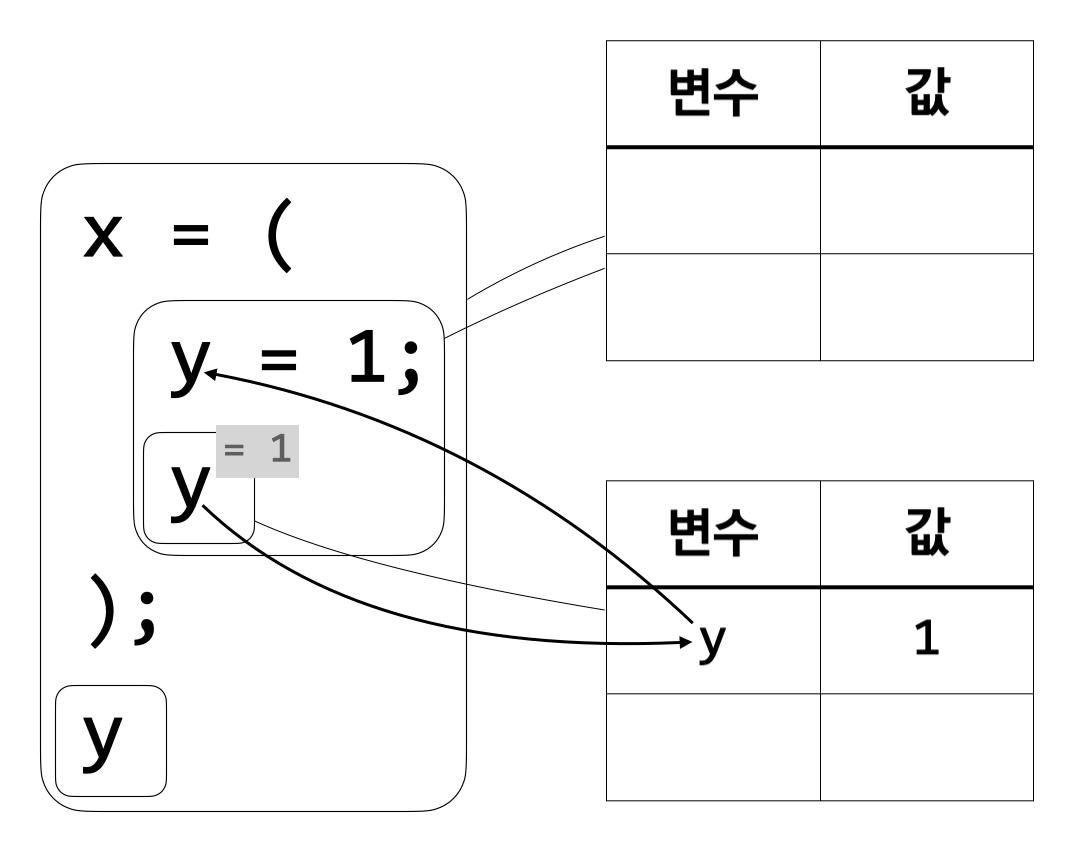
환경으로부터 \(\tt y\)의 값이 1임을 알 수 있으므로 \(\tt y\)를 계산하면 1이 나온다.

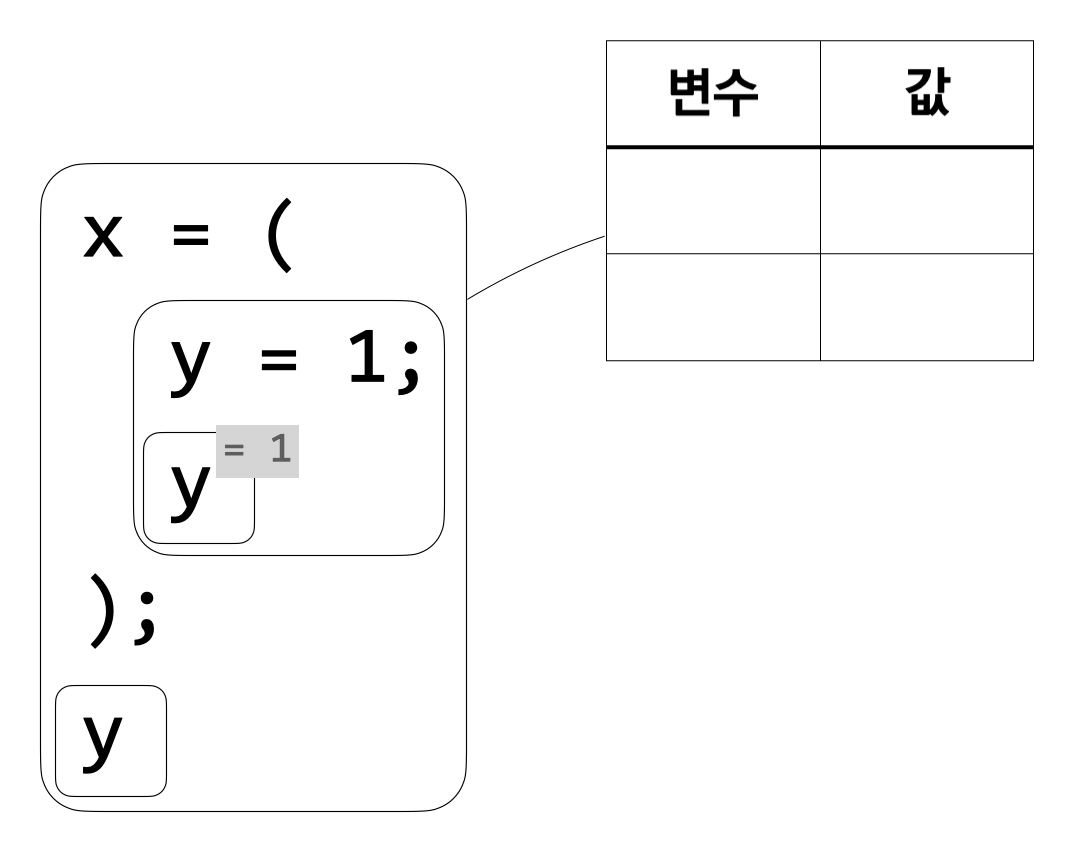
이제 \(\tt y\)의 값을 사용할 수 있는 구간이 끝났으므로 \(\tt y\)의 값을 저장한 환경은 더 이상 필요 없다.

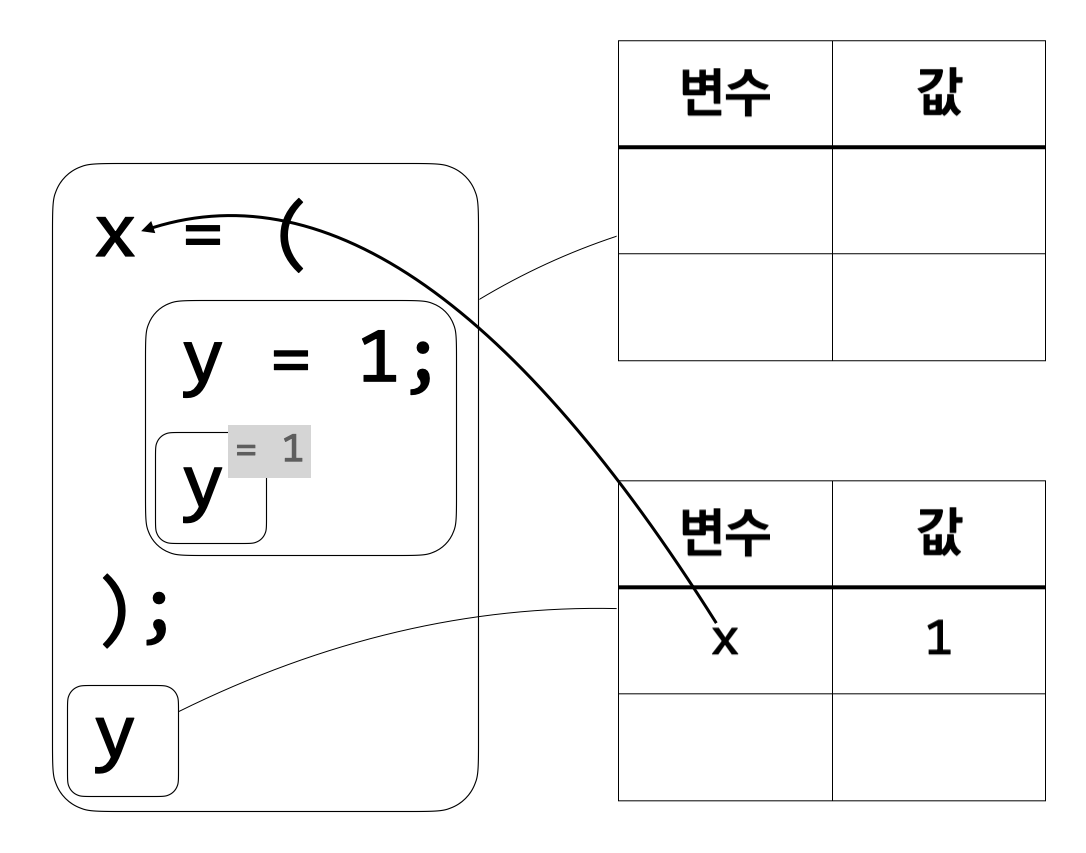
\({\tt y} = 1; {\tt y}\)의 계산 결과가 1이므로 변수 \({\tt x}\)의 값이 1이다. \({\tt x}\)의 값을 마지막 \(\tt y\)를 계산할 때 사용할 수 있도록 새 환경을 만든다. 그 후 \(\tt y\)를 계산하려 하면 환경에 \(\tt y\)가 없으므로 마지막 \(\tt y\)가 자유 변수임을 알 수 있다.

산술x의 의미에 따라 계산해도 동일하게 마지막 \(\tt y\)가 자유 변수임을 알 수 있다. 빈 환경에서 \({\tt x} = ({\tt y} = 1; {\tt y}); {\tt y}\)의 실행 결과를 구하려면 먼저 빈 환경에서 \({\tt y} = 1; {\tt y}\)의 실행 결과를 찾아야 한다. 그 결과는 \(1\)이다. 그럼 남은 일은 빈 환경에 \({\tt x}\)의 값이 1이라는 정보를 추가하여 \([{\tt x}\mapsto1]\)라는 환경을 만들고 그 환경에서 \(\tt y\)를 계산하는 것이다. 보다시피 \([{\tt x}\mapsto1]\)에는 \(\tt y\)가 없다. 마지막 \(\tt y\)는 자유 변수인 것이다. 이처럼, \(x = e_1; e_2\) 형태로 변수를 정의했을 때, 그 변수의 영역은 \(e_2\)만을 포함하며, \(e_1\)은 물론이고 전체 식에서 \(e_2\)가 아닌 어떤 부분도 변수의 영역에 들어가지 않는다.